National Pi Day

Pi Day is a celebration of the mathematical constant "pi" (or π in Greek)."

Pi Day is celebrated on 3/14 every year because 3, 1, and 4 are the first three digits of pi.

3/14 is also Albert Einstein's birthday, who was born March 14, 1879.

The first celebration was held in San Francisco - and in it mathematicians walked around a circular room eating pie!

Fun Facts about Pi

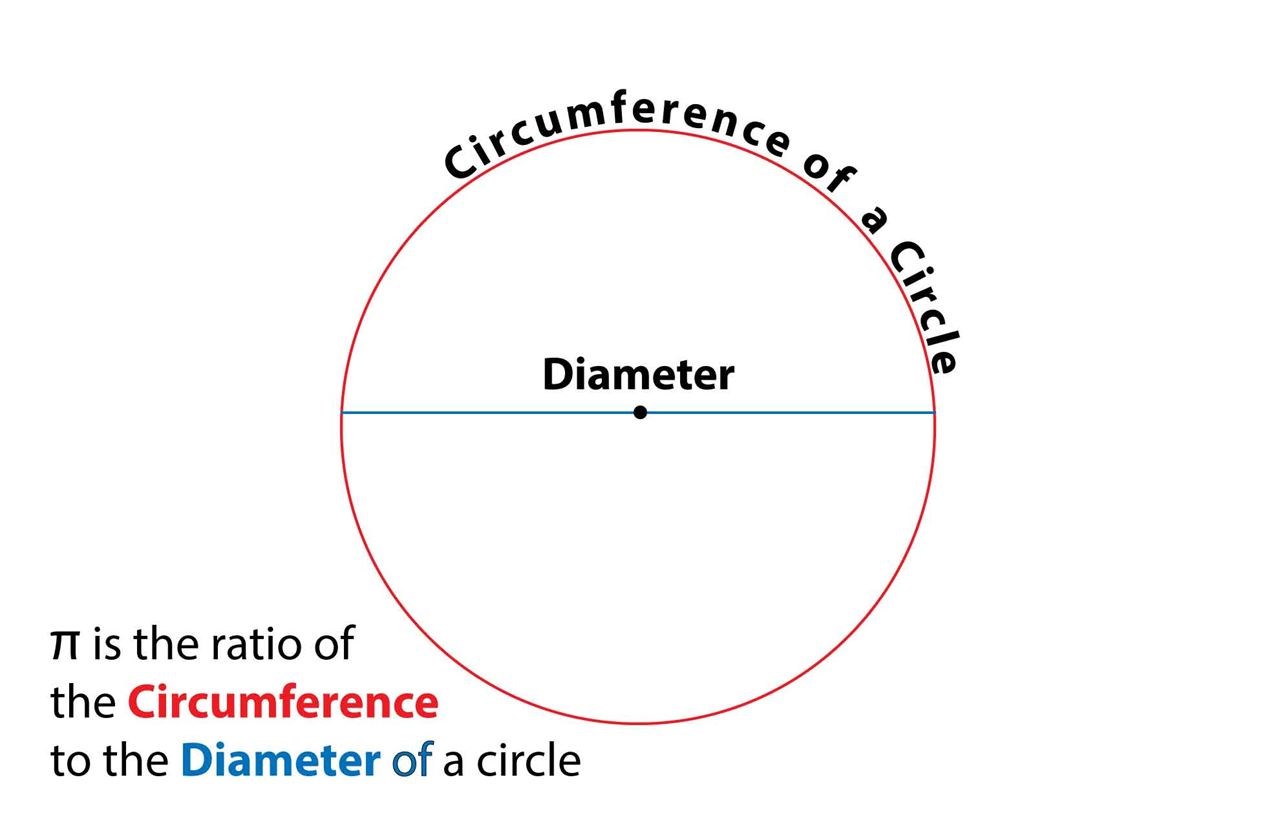
Pi is the ratio of a circle's circumference (the length of the circle) to its diameter (any straight line that passes through its diameter).

Pi is constant -- that is, it (the ratio) is the same for any circle.

Pi never ends. That is why it is usually represented as "3.14..."

In Proposition 3 of his treatise Measurement of a Circle, Archimedes showed that pi had a value between greater than 223/71and less than 22/7. That is why July 22 (7/22) is called "pi approximation day"!

Learn about Archimedes who first calculated Pi in 250 BC

Archimedes of Syracuse

By: Joey from Greendale

Archimedes of Syracuse was an early Greek mathematician, astronomer and inventor.

Archimedes

By: Collin from Liberty Township

Archimedes is important to me because some of his studies, inventions, and principles have a base in modern day science, math, physics, engineering, and astronomy.

Science Hero: Archimedes of Syracuse

By: Joey from Greendale

The Classical Greek mathematician and engineer whose inventions helped establish geometry and calculus.

Advanced Facts about Pi - Egyptians Approxmate Pi

The Egyptians

A circle is a shape, made up of the infinite number of points equidistant from the center of a circle. Unlike a straight line, it is hard to measure a circle! That is the essence of the problem of pi.

Polygons are figures made up of lines, and hence easy to measure. The ancient Egyptians approximated pi by comparing a circle to something they could measure, a polygon.

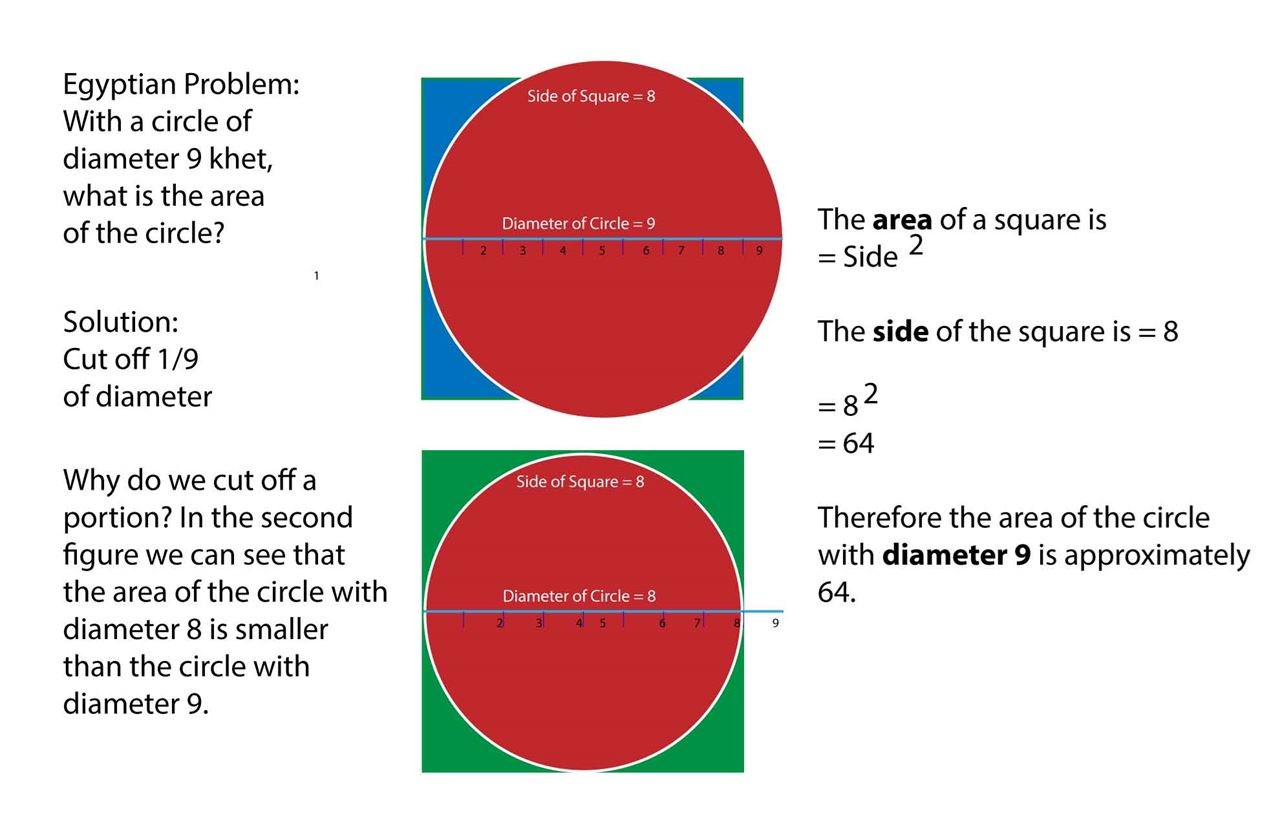
The evidence for Egyptians approximating pi originates in the Rhind Mathematical Papyrus (1650 BC). Math scholars differ in their interpretations of the text. Here is one reading: In one section, the Egyptian scholar Ahmes poses a problem: if you have a circle with a diameter of 9 khet, what is its area?

Now khet is a measure like inch or feet, so we aren't too worried about that. And, as you can imagine, there are different polygons that can have the same diameter as a circle, such as a square or a polygon.

The area of a square with a side corresponding to the diamter 9 would be d2, or 92 = 81. But the square is bigger than the circle. The scholar Ahmes takes 1/9th of the diameter, and gets the number 8.

He thens squares the number 8 which gives 64. So, 64 is the area of a circle that has a diameter of 9. Modern scholars calculate pi from this, and some believe the Egyptian value for pi was 3.126 -- pretty close to 3.14!

Advanced Facts about Pi - Archimedes Calculates Pi with an Algorithm

It was the great mathematical genius Archimedes of Syracuse who created a new way of accurately calculating pi.

Archimedes created an algorithm to calculate pi. What's an algorithm? Just a series of steps, like a recipe.

Instead of just doing one calculation, he used the results of the first calculation and repeated the steps to get a more and more accurate calculation of pi. This is called an iterative process.

In the Egyptian example above, we could see that a circle with diameter 8 would be smaller than a square with side 8. We also could see that a circle with diameter 9 is larger than a square with side 8.

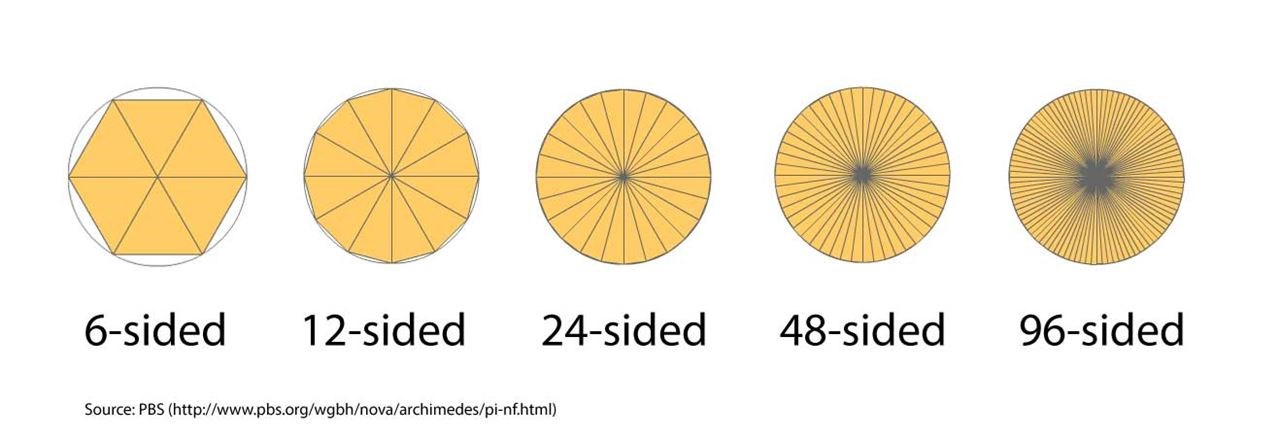
Similarly, Archimedes used polygons both inside (inscribed) and outside (circumscribed) a circle to get closer and closer to the area of the circle--and find pi, the ratio of the circumference to the diameter.

He first used a 6-sided polygon, then doubled the number of sides to make a 12-sided polygon. What do you think came next?

He then used a 24-sided polygon, a 48-sided polygon, and finally a 96-sided polygon to get closer to the area of the circle--from which you could find the ratio of the circumference to the diameter. In other words, pi!